Assuming That the Chinese Population Continues to Grow at the Same Rate
Assuming that the world population continues to grow at its current rate, how many years would it take for the world population to grow: First, what is Ihe world RNI according to World Population Datasheet? htte Iprborg Publications DataSheets/2016/2016-world-population-data-sheet aspx RNI CBR CDR 20-8 "12 (per 1000) 296 0.012 0.012 is the value of-r" that you will use in the calculations belw Remember; net migration is 0 at the global level, s0 the rato of natural increase (RNI) Is the growth rate (r) for the world populalion; Second, what the size of the world population in 2016. according the World Population Dalasheet? Pzprs 2418.000,00Q Now, use the Exponential Growth Rate formula and solve for n How long would it take to grow by 50%? How long would it take to quadruple? How long would it take to add the next billion?

Related Question
The current world population is about 7.5 billion people The world has current gronth rate of 1.6% per year. Find complete model that gives the world population in billions , after years: How long will take the world population t0 double? How long alter doubling will it take for the workd population to double ngain?
Discussion
You must be signed in to discuss.
Video Transcript
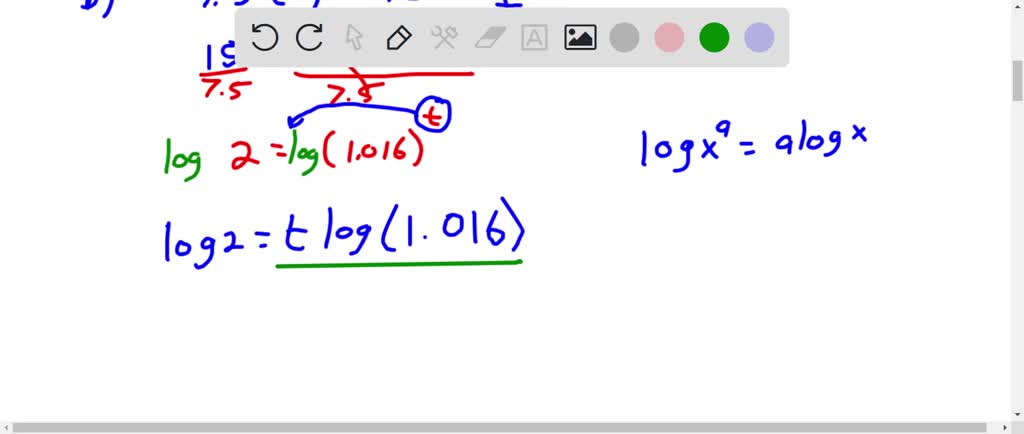
So in this problem we are told that the current world population is about 7.5 billion and it's growing at a rate of 1.6% per year. So the first thing we want to do is to find a model that's going to give us the world population in millions after two years. Okay, well in this case because it's increasing by 1%, this is going to be represented by an exponential model. So our model is pft the population after two years is equal to piece of zero. The initial population times one plus R r rate I'll raise to the T power. Well in this case we know the initial population, it's 7.5 billion. So they will substitute that it now for our rate we have to take our percent and change it to a decimal. So we move the decimal .2 places to the left. So we'll have 0.016 all raised to the T power. Well we can simplify that one plus. 0.16 is just 1.16. So our function will be pft equals 7.5 times 1.16. All raised to the T power. So that's the end of the party now in part B we want to know and how many years or how long is it going to take to double the population? Well first off, if we have 7.5 billion people now and we multiply that by 27.5 times two would equal to 15 billion. So 15 would represent our population. In other words that's our pft value. So what we can do is we can go ahead and substitute 15 in place of pft. So we're gonna have 15 equal to 7.5 times 1.016. All raised to the T. Power. So now what we just need to do is solve this equation for T. So I'll begin by dividing both sides of our equation by 7.5 And 15 divided by 7.5 is too, so this is equal to 1.016 raised to the T. Power now because we can't rewrite both sides with the same base. I'm going to take the log of both sides of our equation because one of our properties for logs said that the log of X raised to the A power is equal to eight times the log of X. So on the right hand side we can take our exponents and multiply it by the log of our base. So in other words we're going to have the log of two Equal to T. Times the log of 1.016. And I apologize there, it's kind of lagging a little bit. So the log of it lets me right here, 1.016. Alright, now we can finally write a little bit. Okay so now to solve for T. All we need to do is go ahead and divide both sides of our equation by the log of 1.016. It's a log of 1.016. Okay perfect. So now that will isolate the tea. We can go ahead and type this into our calculator. So we're gonna have the log of two getting divided by the log of 1.016. And in this case it doesn't look like you were told what's around two. So I'll just round two places after the decimal. So you'll find it will take approximately 43.67 years. That's the answer to the party. Now for part C. What they want us to do is to determine how long after doubling will take for the world population to double again. So we can do this in a couple of different ways. So the way I'm going to approach it is if we're doubling it again, that means compared to our initial population it's four times in Well 7.5 times four is equal to 30. So that would be our pft value. So 30 would equal to 7.5 Times 1.016 raised to the T. Power. So we can solve in the same manner. So we'll divide both sides of our equation by 7.5 And 30 divided by 7.5 is four. So this will equal to 1.016 raised to the T power. Just like we did before we're now going to take the log of both sides. Because now on the left hand side or sorry on the right hand side of our equation we can use that property for log And go ahead and rewrite this. So we're going to have the log of four and I apologize for the messy handwriting here. So like I said we're gonna have the log of four again if it lets me start writing I will here we go. So log of four equal to t times the log of 1.016. So just like we did before we're gonna divide both sides of our equation by the log of 1.016. Alright so now let's go ahead and use our calculator. We're going to have the log of four Getting divided by the log of 1.016. And in this case what you'll find is that T will equal to 87.33. Now keep in mind the wording of the problem, it says how long after doubling would take. Well remember in part B we found it would take 43.67 years. And now we found it would take 87.33 years. So the find the difference will just subtract those. So 87.33 -43.67. Well 87.33 -43.67 is equal to 43.66. So that's how many more years it will take.
Source: https://www.numerade.com/ask/question/assuming-that-the-world-population-continues-to-grow-at-its-current-rate-how-many-years-would-it-take-for-the-world-population-to-grow-first-what-is-ihe-world-rni-according-to-world-populati-53775/
